









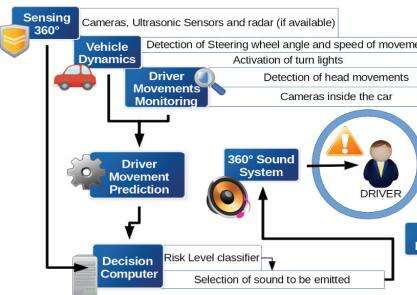
在智能驾驶控制中,驾驶员模型的意义显得尤为重要。通俗的讲,我们可以将驾驶员理解为一个具有反馈控制的系统。驾驶员可以基于自己预瞄的路径和期望的路径的差值形成一个反馈闭环系统。常用的反馈闭环系统会考虑驾驶员的一些特性参数。比如用PID来映射驾驶员,用比例控制P来表示驾驶员输入的方向盘转角(油门开度),用微分I来表示驾驶员的预瞄控制,用积分D表示驾驶员的延迟(反应延迟、肌肉延迟等等),而反馈的输入为路径差值,这样既可形成一个预瞄反馈系统,这样的预瞄系统属于单点预瞄系统。而多点预瞄系统是针对大曲率的路径的控制模型,驾驶员模型根据靠近车点的期望路径曲率和远视点的期望路径曲率,来修正方向盘转角(油门开度),从而控制车辆在期望的路径上行驶。多点预瞄系统与单点预瞄系统的区别在于,单点预瞄系统的反馈输入为预瞄路径和期望路径的横坐标之差,而多点预瞄系统的输入为航向角的偏差值。其中,预瞄路径是根据车辆当前的朝向及航向角预瞄准的一条路径。
车辆控制中通常需要坐标转换,下面来简单探讨下全球坐标模型:
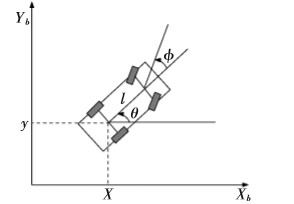
全球坐标系
在全球坐标系下,通过4个重要参数来表达汽车的方位信息。其中,(x,y)为汽车后轴的中心坐标值,θ为汽车与x轴之间的夹角,Φ为车辆前轮的转向角(与方向盘转角对应)。
由此,我们可得到车辆运动学方程为:
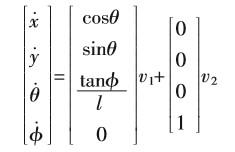
其中,V1为车辆后轮速度,V2为车辆转向速度。
相对于全球坐标系下的车辆运动学方程,基于道路坐标系的更加适合车辆控制。其原因在于传感器更易于获取道路的信息,比如摄像头获取车道线信息。基于道路坐标系的车辆主要参数如下图所示:
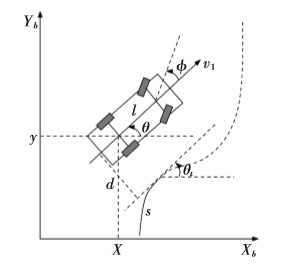
道路坐标系下的车辆模型图
其中,s为车辆从起始点开始所行使的路径长度,d为车辆后轴与目标道路(路径)之间的垂直距离,`θ=θ-θt为车辆与路径之间的角度,(即曲线路径 的弧长)。

我们需要的道路曲率为:
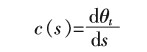
从式中,我们可以看到省略了车辆转向速度V2,从而简化了模型。
通过模型转换,可以得到:

其中,
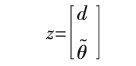
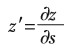
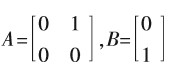
从而我们可以得到以下的驾驶员模型:
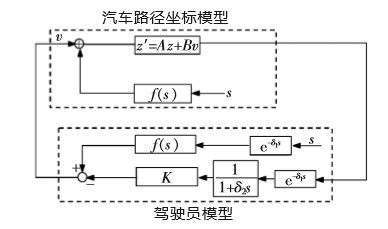
路径跟随闭环控制系统框图
从上图可知,驾驶员可以模拟为一种以道路信息作为反馈的智能自适应控制器。
以上内容供读者参考学习。
(END)