









1.某一个神经元运行流程

单一神经元的结构如图所示。
首先,使用x与w相乘,开始的时候是随机的给定w的值;
然后,将乘积与偏执b加起来,对于b的理解是就像一元线性回归中的常数项,是用来修正值的。
其次,将和带入激活函数;
最后,将激活函数的值计算损失值,也就是与真实值之间的差异,最终的目标是损失值越小越好。
2.激活函数
常用的损失函数有两种一种是Sigmoid,另外一个是relu。
(1)Sigmoid
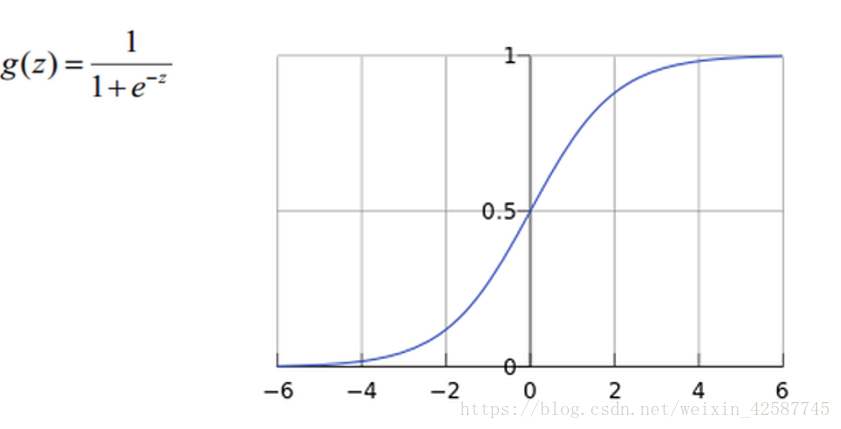
首先,其值的范围为0-1之间;
然后,进过e的-z的变换,e的x次方的函数本来是随着x的增加而增加的,但是e的-z次方代表的是随着z的增加而减小,但是最后又进行了一个到数处理,结果还是随着x的增加而增加,并且将值限制在了0-1之间了。但是Sigmoid损失函数仅适合于在分类算法中使用,不适合在回归算法中使用,因为其结果值在0-1之间,值太小,几乎接近与0 ,在回归中很容易导致 梯度消失。
(2)Relu

首先,relu函数是一次函数,并且值随着自变量的增大而增大,同时方便在求梯度时方便求导。
其次,因为没有值的大小限制,并且求导较为容易,因此常用与在回归中使用。
3.损失函数
3.1 损失函数
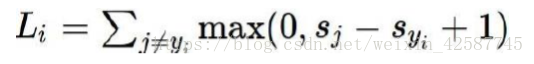
损失函数经过激活函数后的值(预测值)与真实值之间的差异,对其求和既是总体的损失值,但是可在后面+1处理。
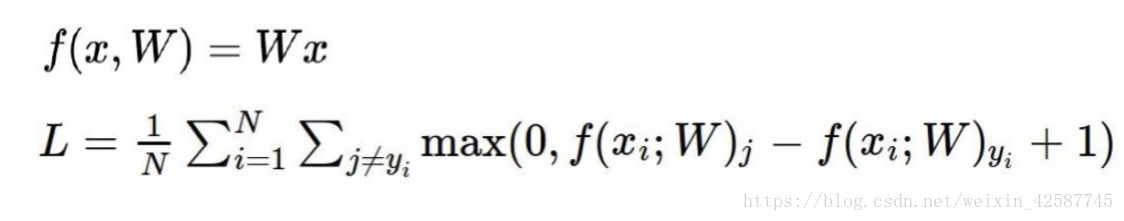
损失值不应该与样本的个数有关,因此需要对其求平均值。
3.2 正则项
3.2.2 正则化
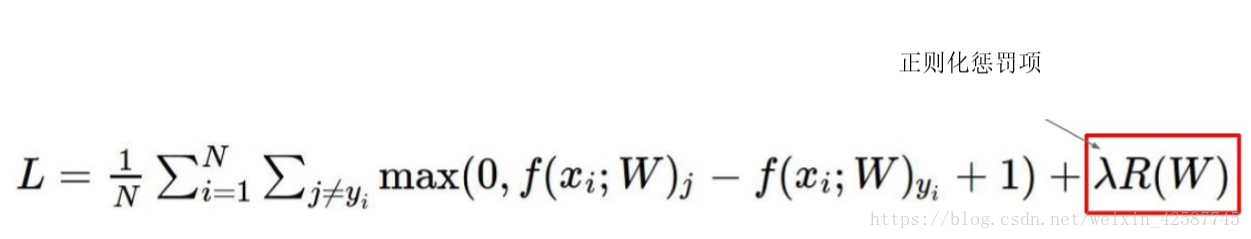
神经网络常用L2惩罚项,其目的是:对损失函数更合理,比如:
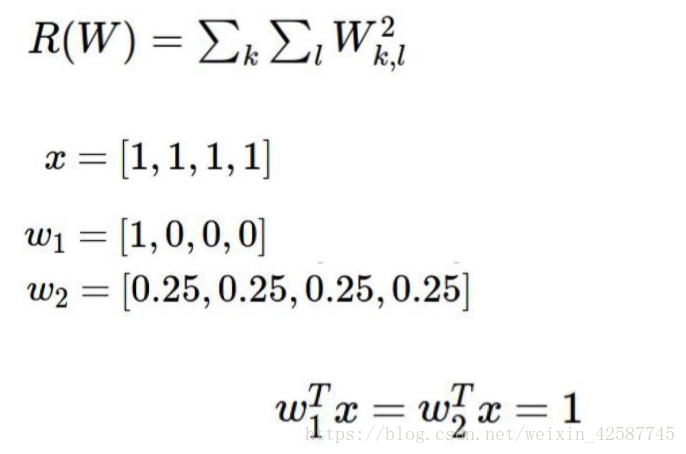
对于该情况,x与w1的乘积的结果与x与W2的乘积的结果相同,但是对于w1的理解为,因为x的第一个数的权重为1,因此每次都是看中的x的第一个值,x的其余的值不看,也即是每次只是看中一个特征;而w2代表的是x的每个值都看中,每个特征都要考虑。因此w2的权重赋值较w1要好,但是最终计算出来的值是一样的,如何区分?如何表示?
因此权重值的范围都是在0-1之间, 因此就可使用正则化处理,全考虑的情况的w平方的值与只考虑一部分特征的的w方的值较小,因此在损失函数的最后面添加一个正则化项。
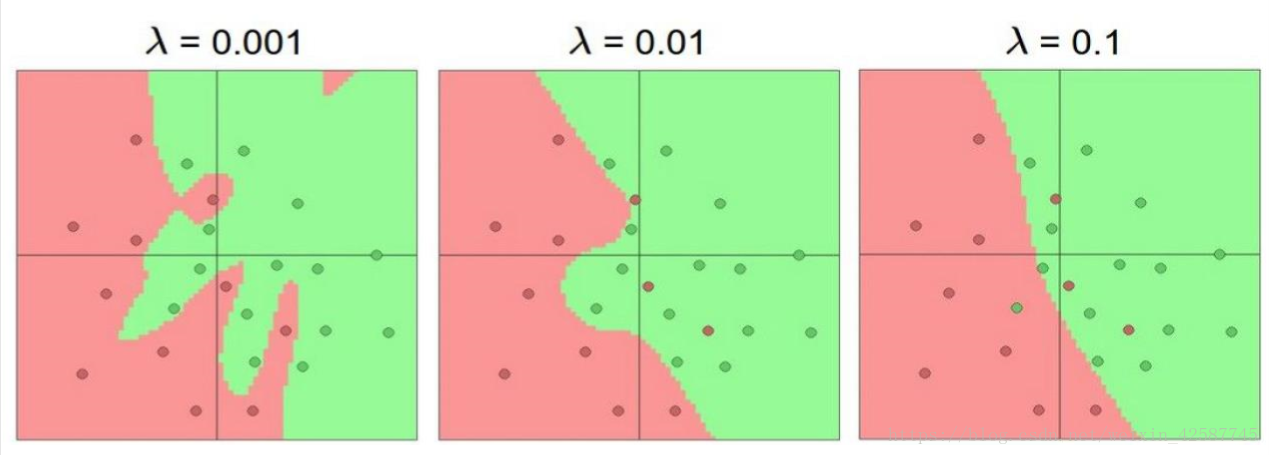
3.2.2 入的值
入 的值是对正则化的限制,限制正则化的作用为多大,并且并不是入的值越小越好,因为越小会产生过拟合。一般选择0.01.
4.反向传播
反向传播是当发现该种权重值情况下,损失函数值较大时,就要方向回去从新修改w的值,以致最终的损失值到达要求。
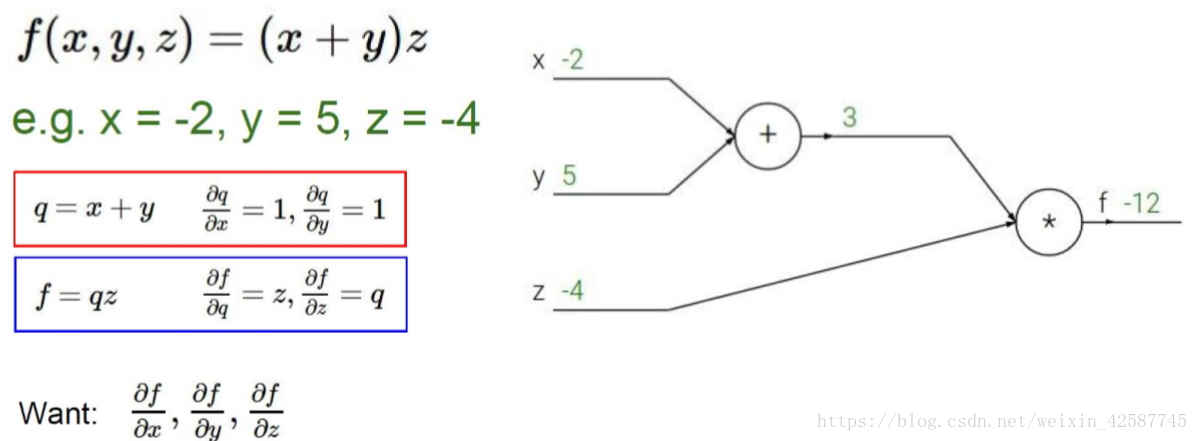
这里的-2/5/-4就相当于神经网络中的权重,若想知道x/y/z分别对f起多大作用,则只需用f对其求分别求偏导, ,然后根据x/y/z目前对f的影响的大小结合损失值的大小来对w进行调整。
既是:

5.梯度下降法
梯度下降指的是,我们在修改w的值时,损失值的减小的速度,但是速度最大既是沿着起点和目标点之间的斜率方向才能好满足,既是:沿着斜率的方向走到目标点的时间最短。
5.1 Bachsize
通常是取2de整数倍(32.64,128)
6.学习率
学习率是值,我在在设置梯度下降时的一个步长,当步长过大,中间就会省略很多信息,并且不能保证在这段距离中是否是按照斜率的方向在下降。
7.隐藏层的个数(神经元的个数)

在实际操作过程中,当准确率达不到时,可以选择添加神经元的个数,但是并不是神经元的个数越多越好,因为也会发生过拟合。
8.网络结构
神经网络可以看成是由许多个激活函数单元叠加而成,最简单的神经网络是一个二层神经网络,如图所示。
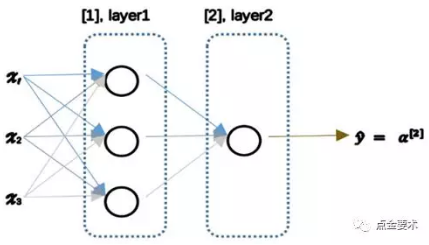
二层神经网络
在这个网络结构中,一共有2层:1个隐藏层,1个输出层。其中第一层为隐藏层,有3个激活单元。第二层为输出层,有1个激活单元。
将上图所示的二层神经网络左半部遮住,结果如下图所示。该神经网络的右半部其实是以按照逻辑回归的方式输出。
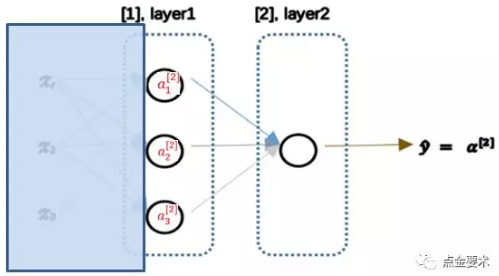
从神经网络的输出层来看,其本质与逻辑回归无二,只不过是将逻辑回归模型中的输入向量x = [x0,x1,x2,x3]变成神经网络隐藏层的输出
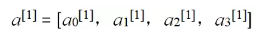
。我们可以把a看成是更高级的特征值,即x的进化体,并且是由x决定的。由于梯度下降,这些更高级的特征是a变化的,并且会变得越来越厉害,所以这些更高级的特征值远比仅仅将x几次方更厉害,也能更好的预测数据。
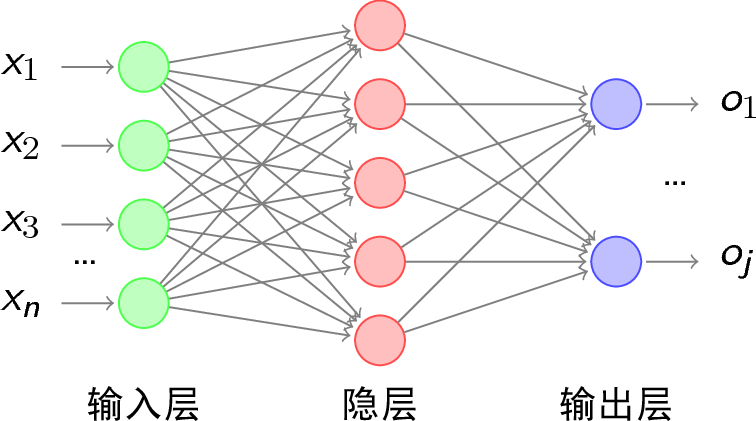
BP神经网络的结构

1. 通常一个神经网络由一个输入层,多个隐藏层和一个输出层构成。
2. 图中圆圈可以视为一个神经元(又可以称为感知器)。
3. 设计神经网络的重要工作是设计隐藏层,及神经元之间的权重。