









众所周知,PID是车辆控制中常见的算法,也是一种非常经典的控制模型。本文将着重讲解PID。
何为PID?
P:Proportion,比例控制,可通俗理解为一个比例系数;
I:Integral,积分控制,可通俗理解为使误差降为0而调和的参数;
D:Derivative,微分控制,可通俗理解为最快获得最优解的参数。
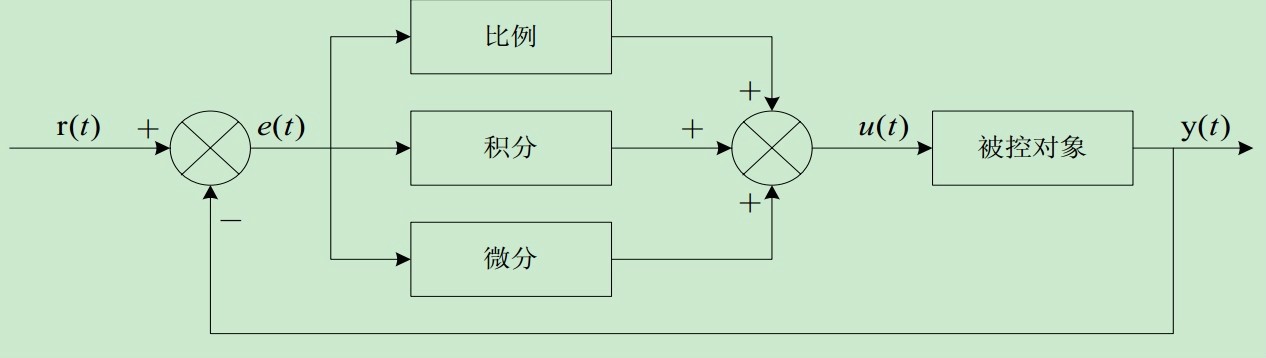
PID框图
PID需要由被控对象的偏差来做模型输入,被控对象偏差=被控对象输入值-目标设定值。比如,ACC的目标车速为100kph,而实际测到的车速为98kph,则100kph为目标设定值,97kph为被控对象输入值,被控对象偏差为3kph。
P比例控制是一种最简单的控制方式,模型的输出与被控对象偏差信号成比例关系。假设,我们要控制一爬楼梯机器人,目标要爬100层楼梯,而Kp(P)的值为99,此时,我们可以得到结论:机器人一下可以走到第99个楼梯上,无论如何都无法走到第100个楼梯上,即存在稳态误差。如果Kp(P)的值是9,那机器人依然可以走到第99层,也无法走到第100个楼梯上,需要更多的控制循环方能走到第99个楼梯上。从而我们可以知道,比例系数Kp的作用是加快系统的响应速度,提高系统的调节精度。Kp越大,系统的响应速度越快,但也越容易产生超调,甚至可能会导致系统不稳定;Kp越小,系统的响应速度越慢,延长调节时间,使系统动态特性变差。
PI控制,即为比例+积分控制,当按照一定的爬楼梯步伐走到第101楼梯,然后又回头走到第99楼梯上,在第100楼梯处来回震荡几次后走到目标位置处。从而我们可以知道,在积分I控制过程中,系统的输出与被控对象偏差信号的积分成正比关系。对一个自适应系统来说,引入积分项可消除稳态误差。积分项对误差的影响取决于时间的积分,随着时间的增加,积分项会变大,此时,积分项会随着时间的增加而加大,进而推动系统的输出增大,使稳态误差变小,直到等于0。因此,Ki(积分系数)的作用是消除系统的稳态(静态)误差,Ki越大,系统的静态误差消除越快;Ki过大时,响应过程的初期会产生积分项饱和现象,从而引起响应过程的超调;Ki过小时,使系统静态误差难以消除,影响系统的调节精度。
PD控制,即为比例+微分控制,当按照一定的爬楼梯步伐走到第103楼梯后慢慢往第100楼梯处走。如果最后能精确停在第100楼梯处,说明没有误差出现,如果停在第100楼梯附近(如第99楼梯处或第111楼梯处),说明系统有误差。从而,我们可知,在微分控制D中,系统的输出与被控对象的偏差信号的微分(偏差的变化率)成正比关系。微分系数Kd的作用是改善系统的动态特性,其作用主要是在响应过程中抑制偏差向任何方向的变化,对偏差变化进行提前预报。Kd过大时会延长调节时间,会降低系统抗干扰性。
以上内容供读者参考学习。
(END)